Critical t-value calculator
The critical t-value calculator allows you to calculate this without using a table. Compare the result of the t-value and the critical value to verify the hypothesis. The critical value (tα) is determined from the tables. It defines the border of the critical area. Depending on the t-value distribution with k-degrees of freedom (one or two tailed), it cuts off part of the probability area on one side or both sides. This critical value is determined on the basis of the number of degrees of freedom and the adopted level of significance. The next step is to check if the | t | > tα condition is met. So we check if the value of t-value is in the critical value. There may be two situations:
- T-value is in the critical area. In this case, the null hypothesis (H₀) should be rejected and an alternative hypothesis (H₁) adopted.
- T-value is not in the critical area. For this reason, there is no reason to reject H₀.
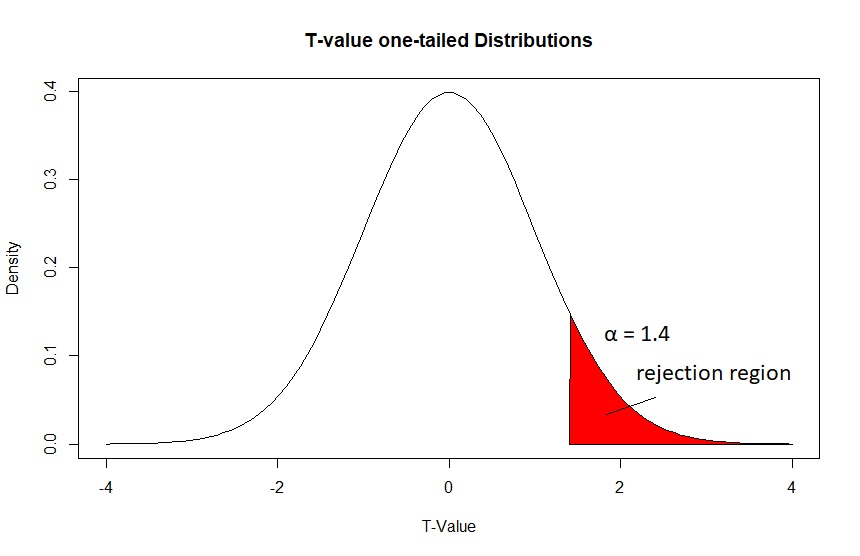
Critical t value calculator for the one-tailed test of hypothesis
Examples: We have a t-value of 1.8. We want to check the critical value for 20 degrees of freedom and a confidence level of 0.05. As a result, we get tα = 1.725. We check if the equation holds |1.8| >1.725. Because t = 1.8, the value of the statistic is in the critical area. Therefore, we conclude that: At a significance level of 0.05, reject the null hypothesis in favour of the alternative hypothesis.
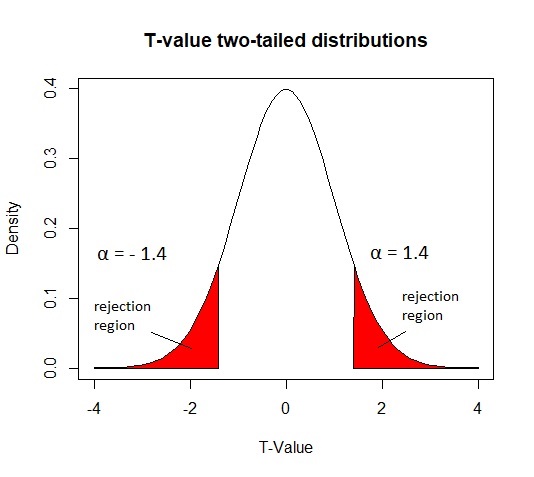
Critical t value calculator for the two-tailed test of hypothesis
Examples: having the t-value equal to 0.6 we want to check the critical value ta for 15 degrees of freedom and the significance level 0.03. We get the tα = 1.074, then we check if |t|> tα, we can see that T is less than tα. We can therefore conclude that at the significance level of 0.03 there are no grounds for rejecting the null hypothesis.
T distribution table for computing critical values
| Df/one tail | α=0.25 | α=0.1 | α=0.05 | α=0.025 | α=0.005 |
| Df/two tails | α=0.5 | α=0.2 | α=0.1 | α=0.05 | α=0.01 |
| 1 | 1 | 3.078 | 6.314 | 12.71 | 63.66 |
| 2 | 0.816 | 1.886 | 2.92 | 4.303 | 9.925 |
| 3 | 0.765 | 1.638 | 2.353 | 3.182 | 5.841 |
| 4 | 0.741 | 1.533 | 2.132 | 2.776 | 4.604 |
| 5 | 0.727 | 1.476 | 2.015 | 2.571 | 4.032 |
| 6 | 0.718 | 1.44 | 1.943 | 2.447 | 3.707 |
| 7 | 0.711 | 1.415 | 1.895 | 2.365 | 3.499 |
| 8 | 0.706 | 1.397 | 1.86 | 2.306 | 3.355 |
| 9 | 0.703 | 1.383 | 1.833 | 2.262 | 3.25 |
| 10 | 0.7 | 1.372 | 1.812 | 2.228 | 3.169 |
| 11 | 0.697 | 1.363 | 1.796 | 2.201 | 3.106 |
| 12 | 0.695 | 1.356 | 1.782 | 2.179 | 3.055 |
| 13 | 0.694 | 1.35 | 1.771 | 2.16 | 3.012 |
| 14 | 0.692 | 1.345 | 1.761 | 2.145 | 2.977 |
| 15 | 0.691 | 1.341 | 1.753 | 2.131 | 2.947 |
| 16 | 0.69 | 1.337 | 1.746 | 2.12 | 2.921 |
| 17 | 0.689 | 1.333 | 1.74 | 2.11 | 2.898 |
| 18 | 0.688 | 1.33 | 1.734 | 2.101 | 2.878 |
| 19 | 0.688 | 1.328 | 1.729 | 2.093 | 2.861 |
| 20 | 0.687 | 1.325 | 1.725 | 2.086 | 2.845 |
| 21 | 0.686 | 1.323 | 1.721 | 2.08 | 2.831 |
| 22 | 0.686 | 1.321 | 1.717 | 2.074 | 2.819 |
| 23 | 0.685 | 1.319 | 1.714 | 2.069 | 2.807 |
| 24 | 0.685 | 1.318 | 1.711 | 2.064 | 2.797 |
| 25 | 0.684 | 1.316 | 1.708 | 2.06 | 2.787 |
| 26 | 0.684 | 1.315 | 1.706 | 2.056 | 2.779 |
| 27 | 0.684 | 1.314 | 1.703 | 2.052 | 2.771 |
| 28 | 0.683 | 1.313 | 1.701 | 2.048 | 2.763 |
| 29 | 0.683 | 1.311 | 1.699 | 2.045 | 2.756 |
| 30 | 0.683 | 1.31 | 1.697 | 2.042 | 2.75 |
| 100 | 0.677 | 1.29 | 1.66 | 1.984 | 2.626 |
| Z | 0.674 | 1.282 | 1.645 | 1.96 | 2.576 |
| 50% | 80% | 90% | 95% | 99% |