Log Calculator – Calculate Logarithms with Ease
Log Calculator
Are you looking for a convenient way to calculate logarithms? Look no further! Our log calculator is here to help you effortlessly calculate the logarithm of positive numbers and the number e. With advanced options, you can even calculate logarithms with a root in the base and in the argument of the logarithm. For example, the most commonly used logarithms are log10(x) and the natural logarithm loge(x), or denoted as ln(x).
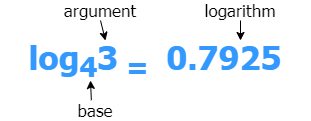
Logarithms, as a rule, are calculated only for positive numbers and different from 1 in the base.
What is a Logarithm?
A logarithm is a mathematical function that represents the exponent to which a base must be raised to produce a given number. It is denoted as logb(x), where b is the base and x is the number. Logarithms have various applications in mathematics, science, engineering, and finance.
Logarithm Rules
Before we delve into the functionality of our log calculator, let’s briefly discuss some important logarithm rules:
- Product Rule: logb(xy) = logb(x) + logb(y)
- Quotient Rule: logb(x/y) = logb(x) – logb(y)
- Power Rule: logb(xn) = n * logb(x)
Common Logarithm and Natural Logarithm
The most commonly used logarithms are the common logarithm (base 10) and the natural logarithm (base e). The common logarithm is denoted as log(x) or log10(x), while the natural logarithm is denoted as ln(x) or loge(x). Both logarithms have their own set of properties and applications.
Properties of Common Logarithm:
- log(1) = 0
- log(10) = 1
- log(xy) = log(x) + log(y)
- log(x/y) = log(x) – log(y)
- log(xn) = n * log(x)
Properties of Natural Logarithm:
- ln(1) = 0
- ln(e) = 1
- ln(xy) = ln(x) + ln(y)
- ln(x/y) = ln(x) – ln(y)
- ln(xn) = n * ln(x)
Using the Logarithm Calculator
Our logarithm calculator provides a user-friendly interface to make your calculations quick and hassle-free. Here’s how you can use it:
- Enter the base value in the designated field. The base represents the number that is raised to the power of the logarithm.
- Enter the argument value in the next field. The argument is the number for which you want to calculate the logarithm.
For advanced options, you can choose to calculate logarithms with a root in the base and/or in the argument. This allows for greater flexibility in your calculations.
Natural Logarithm
The natural logarithm, denoted as ln(x), is a special logarithm with base e. The number e is an important mathematical constant approximately equal to 2.71828. The natural logarithm has wide-ranging applications in calculus, exponential growth and decay, and probability theory.
Log Calculator
Calculating logarithms manually can be time-consuming and prone to errors. Fortunately, there are online logarithms calculators available that can quickly and accurately compute logarithmic values. These calculators allow you to input the base and the number, and they provide the logarithmic value as the output.
Using a logarithms calculator is simple. You just need to enter the base and the number for which you want to calculate the logarithm. The calculator will then display the logarithmic value instantly. This can be particularly useful when dealing with complex logarithmic equations or when you need to calculate logarithms repeatedly.
Log Calculator: Examples of Calculating Logarithms
In mathematics, logarithms are used to solve exponential equations and to represent the relationship between the exponent and the base of a given number.
Example 1: Finding the Logarithm of a Number
Let’s say we want to find the logarithm of the number 100 to the base 10. Using a log calculator, we can simply input the number 100 and the base 10 to get the result. The logarithm of 100 to the base 10 is 2.
Example 2: Solving Exponential Equations
Logarithms can also be used to solve exponential equations. For example, let’s consider the equation 2^x = 16. To find the value of x, we can take the logarithm of both sides of the equation. Using a log calculator, we can input the base 2 and the number 16 to get the result. The logarithm of 16 to the base 2 is 4. Therefore, x = 4 is the solution to the equation.
Example 3: Calculating Logarithmic Functions
Logarithmic functions are commonly used in mathematical modeling and data analysis. Let’s say we have a logarithmic function f(x) = log(base 2) x. To evaluate this function for a specific value of x, we can use a log calculator. For instance, if we want to find f(8), we can input the base 2 and the number 8 into the log calculator. The result is 3, so f(8) = 3.
Example 4: Using Logarithms in Finance
Logarithms are also useful in financial calculations, especially when dealing with exponential growth or decay. For instance, the compound interest formula A = P(1 + r/n)^(nt) involves logarithms. Let’s say we want to calculate the final amount (A) after 5 years, given an initial principal (P) of $1000, an annual interest rate (r) of 5%, and compounded quarterly (n = 4). Using a log calculator, we can input the values into the formula and calculate the result. The final amount after 5 years is approximately $1283.68.
Example 5: Logarithms in Science
Logarithms are widely used in scientific calculations, particularly in chemistry and physics. One common application is in pH calculations. The pH scale measures the acidity or alkalinity of a solution. The pH value is calculated using the formula pH = -log[H+], where [H+] represents the concentration of hydrogen ions in the solution. Using a log calculator, we can input the concentration of hydrogen ions and calculate the pH value.
These examples demonstrate the practical applications of logarithms and how a log calculator can be a valuable tool for performing logarithmic calculations. Whether you are solving exponential equations, evaluating logarithmic functions, or using logarithms in finance or science, a log calculator can simplify the process and provide accurate results.
Conclusion
Logarithms are powerful mathematical functions that have various applications in different fields. Understanding the rules, functions, and properties of logarithms is essential for solving exponential equations and simplifying complex mathematical expressions. The common logarithm and natural logarithm are the most commonly used logarithms, each with its own set of properties. Additionally, using a logarithms calculator can greatly simplify the process of calculating logarithmic values and solving logarithmic equations.
By mastering the rules, functions, and properties of logarithms, you can enhance your problem-solving skills and tackle logarithmic equations with confidence.